Max Planck: A hősugárzás hőmérséklete és entrópiája

Fordította: Sas Klára II. fizikus hallgató, 1997. április

1. Bevezetés és tartalmi áttekintés.

Az irreverzibilis sugárzási jelenségekről nemrég megjelent munkámban a hősugárzás entrópiájának olyan formáját állítottam fel, mely mind a termodinamika, mind a mágneses térelmélet követelményeinek eleget tesz ebben a mérettartományban. Vákuumban, stacionárius sugárzás esetében az entrópiának ez a kifejezése a sugárzás hullámhossza és intenzitása között éppen azt az összefüggést szolgáltatja, melyet az ún. Wien-féle energiaeloszlási törvény ad meg. A továbbiakban kísérletet tettem arra, hogy a sugárzási entrópia kifejezését úgy módosítsam, illetőleg általánosítsam, hogy az még minden elméletileg jól megalapozott termodinamikai és elektromágneses formulát kielégítsen. A sikertelen próbálkozások azonban arra a következtetésre juttattak, hogy a felállított kifejezés, és így a Wien-féle energiaeloszlási törvény is szükségszerűen következik az entrópianövekedés elvének az elektromágneses sugárzási elméletben való alkalmazásából.

Mialatt a Wien-féle törvényt Paschen megfigyelései erőteljesen megerősítették, Lummer és Pringsheim nagyobb hullámhosszakra is kiterjedő méréseiknél nagy mértékű divergenciát tapasztaltak. Ezek az eredmények Thiesent arra indították, hogy a Wien-féle formulát egy másikkal helyettesítse, mely egyrészt mind a Stefan-Boltzmann törvénynek, mind a termodinamikailag megalapozott ún. Wien-féle eltolódási törvénynek megfelel, másrészt Lummer adatait sokkal jobb közelítéssel adja vissza.

Tudvalevő, hogy a megfigyelések és az elmélet közötti ellentéteket csak akkor állapíthatjuk meg minden kétséget kizáróan, ha különböző megfigyelők eredményei összhangban vannak egymással. A megfigyelők közötti eldöntetlen kérdés azonban engem is arra biztatott, hogy áttekinthetően összerakjam és szigorú kritika tárgyává tegyem azokat az elméleti megfigyeléseket, melyek az entrópia fent említett kifejezéséhez vezetnek, és amelyek mindenképpen változtatásra szorulnak, ha a Wien-féle eltolódási törvény nem bizonyul általános érvényűnek. A lényeget szeretném itt röviden közölni, nevezetesen a sugárzási entrópiának egy új kiszámítási módját.

Végül a Wien-féle törvény egy speciális felhasználása következik, melyet 5 mm hullámhosszig az összes pontos mérés bizonyít. Egy kis felületről emittált, majd törő gömbfelületeken áthaladó monokromatikus, koncentrikus sugárnyalábokból álló fénysugár hőmérsékletének kiszámítása.

Ha jól tudom, még mindig akadnak olyan fizikusok, akik azon az állásponton vannak, hogy nem lehet magáról a hősugárzás hőmérsékletéről beszélni, csak annak a testnek a hőmérsékletéről, mely a sugárzást kibocsátja. Eszerint a nézet szerint az előbb vázolt lencserendszerből kilépő sugárzást nem lehetne termikusan magyarázni anélkül, hogy ne vennénk figyelembe keletkezését és továbbterjedését az összes törő felületen. Ez mindenképpen nagyon körülményes és feleleges volna. Mert végül is az a döntő, hogy milyen tulajdonságai vannak a sugárzásnak ott, ahol hatását kifejti. Az egyáltalán nem érdekes, hogy milyen tulajdonságokkal rendelkezett korábban, melyeket később el is veszíthetett. Egyébként az, hogy a sugárzáshoz egy állandó hőmérsékletet rendelhetünk, bizonyos esetekben érezhetően megnyilvánul. Előnyösnek mutatkozik például a Nap effektív, látszólagos hőmérsékletéről beszélni. Ezzel a hőmérséklettel kellene rendelkeznie a Napnak, ha úgy sugározna, mint egy fekete test, és útközben semmiféle energiaveszteség nem lépne fel. A Nap effektív hőmérséklete nem más, mint a napsugarak valóságos hőmérséklete. Ide tartozik még az is, hogy a különböző színű napsugaraknak más a hőmérséklete, mivel a Nap sugárzásának energiaeloszlása eltér a fekete test spektrumától. Minden monokromatikus sugárhoz egy

meghatározott hőmérsékletet kell tehát rendelnünk, melyet a már korábban megadott formulából számíthatunk ki.

2. Az elmélet fizikai megalapozása.

Az itt tárgyalt elmélet Kirchhoff törvényén alapszik. Egy tükröző felületekkel határolt vákuumba különböző részecskéket szórunk tetszőleges kombinációban. Bizonyos idő elteltével egyensúlyi állapot alakul ki, melyet egyetlen paraméter, a hőmérséklet jellemez, a részecskék száma, minősége érdekes módon nem játszik semmilyen szerepet. Stacionárius sugárzási állapotok vizsgálatokor teljesen közömbös tehát, hogy milyen fajtájúak a vákuumba juttatott részecskék. Ha sikerül sugárzó és elnyelő részecskék egy tetszőleges rendszerében egyensúlyi állapotot kimutatni, az csak olyan lehet, amilyent a Kirchhoff-törvény megkövetel.

Ha élünk azzal a szinte magától értetődő és a termodinamika második főtételéből következő feltevéssel, mely szerint létezik természetes sugárzás, az egyensúlyi sugárzási állapot egy speciális esetben könnyen igazolható. Vegyünk egymástól elegendően távollevő, kis csillapítású, nagy hullámhosszúságú, nyugvó lineáris rezonátorokat. Ha tehát feltesszük, hogy a hősugárzás törvényei pusztán az elektrodinamika segítségével megérthetőek, nem marad más hátra, minthogy a Kirchhoff-törvényben szereplő egyensúlyi állapotot a hősugárzással teljes mértékben azonosítsuk.

Nyugvó lineáris rezonátorok feltételezése a mechanikai termodinamika szemszögéből kétségesnek tűnhet, mivel egyensúlyi hőmérséklet esetén a részecskékhez sebességet is kell rendelnünk. De közelebbi megfontolások alapján látható, hogy csak közvetett összefüggés lehet a molekulák gázelméletből következő sebessége és a hősugárzás között. A hőmérséklet nem a molekula átlagsebességét, hanem az egy szabadsági fokra jutó energiát határozza meg. Megfelelő molekulákat választva kísérletileg igazolható, hogy adott hőmérsékleten, bizonyos határok között, bármilyen átlagsebességet ki lehet mutatni, míg a sugárzás intenzitása állandó, és kizárólag a hőmérséklettől függő marad.

Okot adhat az elmélet kétségbe vonására az is, hogy a sugárzási jelenségek irreverzibilitását, és a sugárzási entrópia fogalmát egyedülálló, sőt egyetlen rezonátort vizsgálva vezettem le. A gázelméletben hozzászoktunk ahhoz, hogy az irreverzibilis folyamatok létrejöttét és az entrópia fogalmának bevezetését csak nagy számú molekula vizsgálata teszi lehetővé. Ezt a gondolatot könnyű megcáfolni. A rendezetlenség elve, mely úgy tűník mindenféle irreverzibilis folyamat alapja, egészen más szerepet játszik a gázelméletben, mint a hősugárzás vizsgálatánál. A gázokban a molekulák szabálytalan elrendeződése és sebességeloszlása jelenti a rendezetlenséget, míg vákuumban a számos sugárnyaláb intenzitásának és rezgésszámának rendezetlen változásai szolgáltatnak okot az entrópia fogalmának bevezetésére. Egyetlen egy rezonátor rezgésekor ugyanúgy kifejezésre jut ez a rendezetlenség, mint szabadtéri sugárzás esetében. Mialatt a gázelméletben a kinetikus energiának egy elenyészően kis egysége, egy molekula szabadsági fokára jutó energia képezi a legkisebb egységet, addig a sugárzáselméletben egyetlen rezonátornak van hasonló szerepe. Ennek megfelelően a stacionárius rezgést reprezentálhatjuk a sugárzási térben található, meghatározott sajátperiódusú rezonátorral. A rezonátor rezgése nem lehet egy egységes elemi folyamat, azaz egyszerű szinuszhullám konstans amplitudóval és fázissal, mivel ilyen estben a rezgés energiája szabadon választható lenne, és nem tudnánk entrópiát definálni. A rezonátor rezgése sok kis közel azonas periódusú és konstans fázisú, illetve amplitudójú rezgés szuperpozíciójából áll elő, vagy pedig, ami matematikailag ugyanahhoz vezet, egyetlen konstans amplitudójú, de szabálytalan fázisú rezgés. Mindkét esetben tudunk rendezetlenségről, és ennek következtében a rezonátor entrópiájáról és hőmérsékletéről beszélni.

3. Az entrópia növekedése egy sugárzási térben található rezonátor esetében.

Előző munkámban egy rezonátor és a természetes sugárzás entrópiáját az energia és a frekvencia függvényeként definiáltam, és utána bebizonyítottam, hogy az entrópiának ez a kifejezése tulajdonképpen az entrópianövekedés elvéből következik. Itt most egy általánosan elterjedt utat kell követnünk. A továbbiakban felírjuk az energiamegmaradást és az entrópianövekedést anélkül, hogy feltételezéseket tennénk az entrópia nagyságára, utána pedig megvizsgáljuk, hogy milyen értékeket rendelhetünk a sugárzás entrópiájához, hogy a termodinamikában bevezetett entrópiafüggvény tulajdonságaival rendelkezzen. Ebből a számításból éppen az az érték fog adódni az entrópia nagyságára, melyet korábbi munkámban felhasználtam.

A következőkben előző munkám jelöléseit és feltevéseit fogom használni, azzal a külölönbséggel, hogy az entrópiát nem tekintem az energia függvényének. Az energiamegmaradás törvényét egy n frekvenciájú rezonátorra felírva, a következő egyenletet kapjuk:

(1)

Itt az U a rezonátor energiáját jelenti, t az idő, c a fénysebesség vákuumban, s a rezgés amplitudójának logaritmikus dekrementuma, dW egy kúp végtelenül kis nyílásszöge, melynek csúcsa a rezonátorban helyezkedik el. És végül J, illetve J‘ a rezonátor egyik oldalára eső, egymásra merőlegesen polarizált n frekvenciájú sugárnyalábok intenzitásai, J‘’ és J‘’’ pedig a rezonátor másik oldalán, ugyanebben az irányban kilépő sugárnyalábok intenzitásait jelöli. J‘’ és J‘’’ a következőképpen számítható ki:

(2)

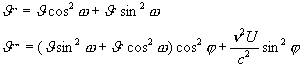
ahol j a rezonátor tengelye és a sugárnyaláb által bezárt szög, w pedig az a szög, amelyet a J-hoz tartozó polarizációsík zár be a sugárnyaláb és a rezonátor által meghatározott síkkal. J‘’ polarizációsíkja a rezonátor tengelyén halad keresztül, J‘’’-é pedig erre merőleges.

Jelöljük a rezonátor entrópiáját a továbbiakban S-sel, a legyen a n frekvenciájú sugárzás intenzitása, így tehát S U-nak és n-nek, míg a J-nak és n-nek meghatározott függvénye. .Az eddigiek alapján felírhatjuk a rezonátort körülvevő térnek dt idő alatt bekövetkező entrópiaváltozását:

Ha ehhez hozzávesszük a rezonátor ugyanezen időtartam alatt bekövetkező entrópiaváltozását, felírhatjuk az első egyenlethez analóg módon a rendszer teljes entrópiaváltozását:

(3)

4. Speciális eset.

Most arra a speciális esetre fogunk rátérni, amikor a rezonátort körülvevő tér folyamatosan stacionárius sugárzási állapotban van folyamatosan. Azt tesszük még fel, hogy a rezonátorra eső sugárzás nem polarizált, függetlenül az időtől és az iránytól konstans, azaz:

Ennek alapján a következőket írhatjuk fel:

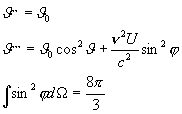
(4) = 0

És végül az entrópia teljes megváltozása, mivel:

(5)

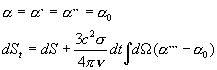
Ha nemcsak a rezonátort körülvevő tér, hanem az egész rendszer stacionárius sugárzási állapotban volna, a rezonátor energiája ebben a speciális esetben a következő lenne:

(6)

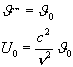
Ekkor az energia és az entrópia független lenne az időtől, ezért -t a rezonátor ‘stacionárius’ energiájának nevezhetjük. Ehhez az értékhez közelít asszimptótikusan az idő haladtával U értéke.

Ha a rezonátor energiája csak kis mértékben tér el a stacionárius értéktől, akkor U-t így is felírhatjuk:

(7)

DU-t a rezonátor stacionárius energiájához tartozó (pozitív vagy negatív) feleslegnek is nevezhetjük, amely nyilvánvalóan arra utal, hogy a rezonátor mennyire tér el egyensúlyi helyzetétől. Ekkor:

(8)

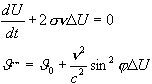
Taylor sorfejtéssel, és DU magasabb hatványainak elhagyásával:

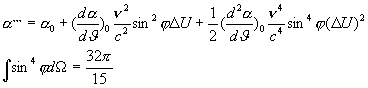
továbbá:

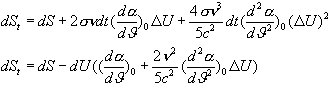
és mivel:

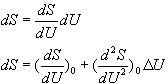
Végezetül, ha az egész rendszer entrópiaváltozását behelyettesítjük, és elhagyjuk DU magasabb hatványait, az alábbi egyenletet kapjuk:

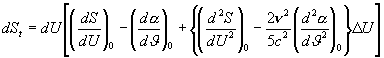
5. Az entrópia szükséges tulajdonságai

Ha az utolsó kifejezés mindig pozitív, mint ahogy a termodinamika második főtétele megköveteli, és mivel dU pozitív és negatív is lehet, DU pedig tetszőlegesen kicsivé tehető, a következő összefüggés mindenütt érvényes:

(9)

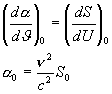
Az integrációs konstanst szabadon választhattuk, mivel nincs fizikai jelentése. Hasonlóképpen folytatva:

(10)

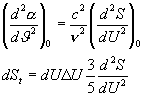
ahol a feleslegessé vált indexet elhagytuk.

Ez a képlet abban az estben fejezi ki az entrópianövekedést, ha a rezonátor állandó sugárzási térben helyezkedik el, U energiája DU kis értékével tér el az egyensúlyi értéktől, és ezenfelül dU nagyságú energiaváltozást szenved. Az entópianövekedés tehát kizárólag dU-tól, illetve DU-tól függ, és ahogy azt már korábban előrebocsátottam, dU és DU arányosak egymással. Mivel DU pozitív, és az előzőek alapján láthatjuk, hogy dU és DU mindig ellentétes előjelű, az utolsó tényezőnek tehát negatívnak kell lennie. Felírhatjuk ilyen alakban:

(11)

ahol f U-nak egy pozitív függvénye, így az entrópianövekedés:

(12)

f(U) függhet a rezonátor n frekvenciájától, a s csillapítási tényezőtől viszont nem, ahogy ezt a (10)-es egyenletből is láthatjuk, hiszen annak baloldala sem tartalmazza s-t.

Kizárólag az entrópianövekedés törvényéből nem vonhatunk le további következtetéseket sem az itt említett speciális, sem általános esetben az entrópia értékére vonatkozóan. Hosszabb számolással azonban, melyet most a rövidség kedvéért mellőzök, bebizonyítható, hogy, ha f U-nak egy tetszőleges pozitív függvénye, és ennek segítségével a (10)-es és a (11)-es egyenletekből kifejezzük S-et U, illetve a-t J függvényében, a (3)-asban megadott mindig pozitív lesz. Mindenesetre leszögezhetjük, hogy az entrópianövekedés törvénye nem elegendő ahhoz, hogy az entrópiát, mint az energia függvényét tárgyaljuk, ehhez az entrópiafüggvény fizikai tulajdonságait részletesebben meg kell vizsgálnunk.

6. Az entrópiafüggvény teljes kiszámítása.

Gondoljuk el, hogy az előbb vizsgált stacionárius sugárzási térben most nem egy, hanem tetszőleges n számú, az eddigiekhez hasonló rezonátor van jelen, melyekben egymástól függetlenül ugyanaz a folyamat játszódik le dt idő alatt. Ekkor a rezonátorok összenergiája nem más, mint az egyes rezonátorok energiájának összege: , az összenergia egyensúlyi értéktől való eltérése: , a dt idő alatt bekövetkező energiaváltozás: , végül pedig az entrópia: .

Első ránézésre azt gondolhatnánk, hogy pontosan úgy függ -től, mint S az U-tól. Ebben az esetben értékét úgyis megkaphatnánk, hogy az S-t kifejező egyenletbe -t helyettesítünk be U helyett. Ezt a feltevést azonban semmilyen fizikai megfontolás nem támasztja alá, hiszen az entrópia nagyságának, ugyanúgy, mint az erőpotenciál pontos értékének, nincs semmi fizikai jelentése. Meghatározott fizikai tartalommal a teljes rendszerben dt idő alatt bekövetkező entrópiaváltozás rendelkezik. Az entrópianövekedés numerikus értéke a folyamat irreverzibilitását, vagy a hővé vált munkát adja meg, és csak ezen pontos értéknek a figyelembevételével tudjuk a megfelelő végkövetkeztetéseket levonni. Az energiaváltozás és az entrópianövekedés közötti szükségszerű összefüggést nem lehetne megérteni, ha nem tennénk fel, hogy az n számú rezonátor entrópianövekedését , illetve teljesen maghatározza. Éppen ebből kifolyólag az entrópianövekedés értékét akkor is megkaphatjuk, ha a (12)-es egyenletbe U helyére -t helyettesítjük be.

Másrészről viszont ez az entrópianövekedés mindenféleképpen megegyezik a (12)-es kifejezés n-szeresével, mivel n egymástól független, azonos esemény játszódik le egyidejűleg. Így a következőket kapjuk:

Ha most helyébe mindenütt U-t teszünk:

melynek megoldása:

vagy a (11)-es alapján:

ahol a C konstans csak n-től függhet.

Ezt kétszer integrálva adódik:

(13)

ahol szintén egy n-től függő konstans, a másik additív konstanst azért nem írjuk ki, mert nincs semmi fizikai jelentése.

Végül a (9)-es kifejezésből:

vagy a (6)-os figyelembevételével és az index elhagyásával:

(14)

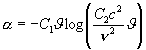
Vegyük most még hozzá a rezonátor hőmérskletének definícióját:

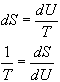
ezek után a (9)-es felhasználásával:

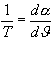
1gy tehát:

(15)

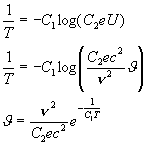
Vezessük be a következő helyettesítést:

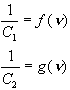
Mivel f(n) és g(n) is arányosak n-vel:

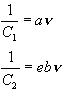
ahol a és b univerzális pozitív konstansok. És végül a (15)-ösbe behelyettesítve:

(16)

F. Kurlbaum és F. Paschen mérései alapján a és b általam kiszámított értékei:

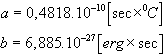
7. A koncentrikus sugárzás hőmérséklete.

Végezetül, mint a Wien-féle törvény egy speciális felhaználását, egy monokromatikus, polarizálatlan fénysugár hőmérsékletét kell kiszámítanunk, melyet egy kis rés emittál a felületre merőlegesen. A sugárzás egy tetszőleges törő gömbfelületekből álló rendszer tengelye mentén halad keresztül. Egy ilyen sugárzás homocentrikus nyalábokból áll, és ebből következően minden törő (vagy tükröző) felület mögött az első emittáló felület valódi, vagy virtuális képét hozza létre, szintén a tengelyre merőlegesen.

Mindenekelőtt tételezzük fel, hogy az utolsó közeg, éppúgy, mint az első, vákuum. Ebben az esetben a hőmérséklet meghatározásához a (16)-os egyenlet alapján elegendő J-t, pontosabban -t, a sugárzás intenzitását kiszámítanunk az utolsó közegben. Könnyű megmutatni, hogy ehhez viszont nem kell más, mint a monokromatikus sugárzás összintenzitása, a képfelület nagysága, valamint a kép egy pontjában a beeső és kilépő sugárnyalábok által bezárt szög.

Múltkori munkámban megmutattam, hogy egy nem polarizált sugárzás esetén, hogyan kaphatjuk meg a frekvenciából a sugárzás intenzitását. Egy ds felületdarabkáról, a tőle r távolságra fekvő felületdarabkára dt idő alatt sugárzott energiamennyiség:

ha a frekvenciaintervallum n és dn közé esik.

Ha az utolsó közegben létrejött kép kis felületelemét ds-val jelöljük, a képre eső monokromatikus sugárzás összintenzitása:

éppúgy energiadimenziójú, mint az előző kifejezés, hiszen dt és dn szorzata skalár.

A második integrál nem egyéb, mint w nyílásszög:

Ha Faz egész képfelület nagysága:

(17)

és ebből a (16)-os felhasználásával megkapjuk a sugárzás hőmérsékletét:

(18)

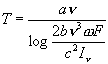
Ha a szóban forgó közeg nem vákuum, hanem n törésmutatójú közeg, az ismert Kirchhoff-Clausius-törvény értelmében a (16)-os egyenletben J helyett J/-et, a (17)-esben pedig I helyett I/-et kell írnunk. A formula tehát általánosan:

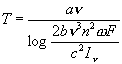
Az így kiszámított hőmérsékletet a sugárzás mindaddig megtartja, míg a közegben zavartalanul terjed, akármekkora utat tesz is meg. Igaz ugyan, hogy nagy távolságban egyre kisebb energiamennyiség halad keresztül egy felületelemen, de ez az energiamennyiség egy annál keskenyebb, a felületelemről kilépő sugárnyalábon oszlik meg, így J értéke változatlan marad. A sugárzás terjedése teljesen reverzibilis folyamat. A sugárzás összegyűjtése egy megfelelő tükör, vagy gyűjtőlencse segítségével történhet.

Vizsgáljuk meg most a sugárzás hőmérsékletét az egyes törő felületek mögött elhelyezkedő közegekben. Minden ilyen közegben a sugárzás egy meghatározott hőmérséklettel rendelkezik, melyet a legutolsó formula alapján kaphatunk meg, ha mindig az adott közegben létrejött valóságos, illetve virtuális képet tekintjük.

A monokromatikus sugárzás frekvenciája természetesen nem változik, és a geometriai optika törvényeiből tudjuk, hogy szorzat is azonos minden közegben. Ha a sugárzás összintenzitása sem változik meg törés vagy visszaverődés esetén, akkor a hőmérséklet is állandó marad, vagy más szavakkal kifejezve: egy koncentrikus sugárzás hőmérséklete törés, illetve reflexió által nem változik meg, feltéve, ha nem lép fel energiaveszteség. Ebben az esetben tehát a törés és a visszaverődés is, éppúgy, mint a sugárzás szabad terjedése, reverzibilis folyamat. De pl. diffúz reflexió esetében, mikor a sugárnyaláb két, vagy esetleg több részre bomlik, a sugárzás összintenzitása megváltozik, ami a sugárnyaláb hőmérsékletének csökkenéséhez vezet. A valóságban minden törés és visszaverődés esetén fellép egy meghatározott energiaveszteség és ezzel együtt hőmérsékletcsökkenés is. Így tehát elvi különbség van aközött, hogy a sugárzás szabad terjedés esetén gyengül le, vagy abszorpció során. Az első esetben a hőmérséklet állandó marad, a másodikban csökken.

Asztigmatikus sugárnyalábok esetén bizonyos fokig analóg törvényszerűségeket lehet megállapítani, a hőmérséklet kiszámítása azonban túl bonyolult formulához vezetne. Bármilyen elhajlás hőmérsékletcsökkenéshez, illetve entrópianövekedéshez vezethet, így a természetes sugárzás elhajlása az irreverzibilis folyamatokhoz tartozik.

Berlin, 1900. március

Max Planck: A Wien-féle egyenlet módosítása.

A mai ülésen Kurlbaum közzétette Rubens-szel végzett legújabb mérései eredményeit. Ezek a nagyobb hullámhosszakra is kiterjedő mérések nyomatékosan megerősítették Lummer és Pringsheim megfigyelésekkel alátámasztott megállapításait, miszerint a Wien-féle energiaeloszlási törvény nem általános érvényű, mint azt eddig sokan gondolták. Ennek a törvénynek korlátai vannak, az ebből adódó egyszerű formula csak rövid hullámhosszakra, illetve alacsony hőmérsékleten ad a tapasztalatokkal egyező eredményt. Mivel én is meg vagyok győződve a Wien-féle törvény fontosságáról, engedtessék meg nekem, hogy röviden itt is szemléltessem, hogy a sugárzás általam kifejlesztett elektromágneses elmélete hogyan viszonyul a megfigyelt tényekhez.

Ez az elmélet az energieloszlásról szóló tételt akkor támasztja alá, ha a besugárzás hatására rezgésbe jött rezonátor entrópiája, mint a rezgési energia függvénye, ismert. Legutóbbi munkámban kiemeltem, hogy az entrópianövekedés elve önmagában nem elegendő ahhoz, hogy ezt a függvényt meghatározzuk. A Wien-féle törvény általánosításához egy különös gondolatmenet, mégpedig egy stacionárius sugárzási térben n egyforma rezonátorból álló rendszer végtelenül kis entrópianövekedésének kétféle módon történő kiszámítása vezetett. A következő egyenletek adódtak:

ahol:

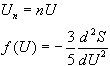
ebből a Wien-féle törvény következő alakját kapjuk:

A függvényegyenletben jobboldalán szereplő kifejezés biztosan a szóban forgó entrópiaváltozást adja, mivel n db. egymástól független esemény játszódik le, úgyhogy ezek entrópiaváltozását csak össze kell adnunk. Ellenben nagyon is elképzelhetőnek tartom, habár nehezen érthető és bizonyítható, hogy a bal oldali kifejezés nem rendelkezik általában az általam korábban feltételezett tulajdonságokkal, vagyis és értékei nem elegendőek ahhoz, hogy a kérdéses entrópiaváltozást meghatározzák, ehhez U értékének is ismertnek kell lennie. Ezt a gondolatmenetet folytatva jutottam el oda, hogy az entrópiához egy teljesen önkényes kifejezést rendeljek, mely bár bonyolultabb a Wien-féle kifejezésnél, mégis úgy tűnik, hogy eleget tesz mind a termodinamika, mind az elektromágneses elmélet követelményeinek.

Az így felálított kifejezések közül egy, amelyik bizonyos feltételek esetén a Wien-féle formulát is visszaadja, különösen szemet szúrt nekem. És mivel a Wien-féle képlet nem elegendő ahhoz, hogy minden megfigyelést alátámasszon, megérdemelné, hogy közelebbről szemügyre vegyük. Tételezzük fel, hogy:

Ez messzemenően a legegyszerűbb kifejezés azok között, amelyek S-t, mint U logaritmikus függvényét szolgáltatják, ezenfelül kis U értékre a Wien-féle képletet is visszaadja. Mivel:

A Wien-féle eltolódási törvényt is felhasználva a következő két konstanst tartalmazó egyenletet kapjuk:

Ez a képlet, amennyire én ezt most át tudom tekinteni, az eddig publikált megfigyeléseket éppoly kielégítően adja vissza, mint az eddig felállított különböző egyenletek. Itt szeretném szíves figyelmüket erre az új formulára felhívni, melyet én az elektomágneses sugárzás elméletének a szemszögéből a legegyszerűbbnek tartok.

Berlin, 1900.október